Studies in Quantum Entanglement Signaling 3-17-2012

Begin forwarded message:
From: JACK SARFATTI <This email address is being protected from spambots. You need JavaScript enabled to view it.>
Subject: Re: dubious about sender control over phi PS
Date: March 17, 2012 6:55:11 PM PDT
To: REK
The no signaling theorem (NST) is violated by
P(g) = (1/2)(1 + |(alpha|alphae^iphi)|^2)
NST demands
P(g) = 1/2
Here are the full details of my calculation for a macro-quantum coherent Glauber state sender Alice entangled with a micro-quantum incoherent single qubit receiver Bob:


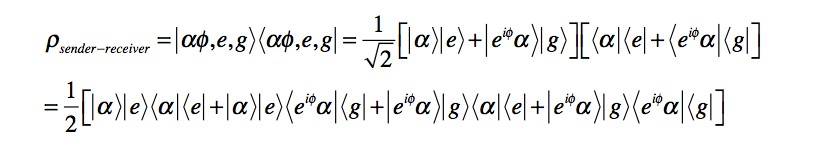
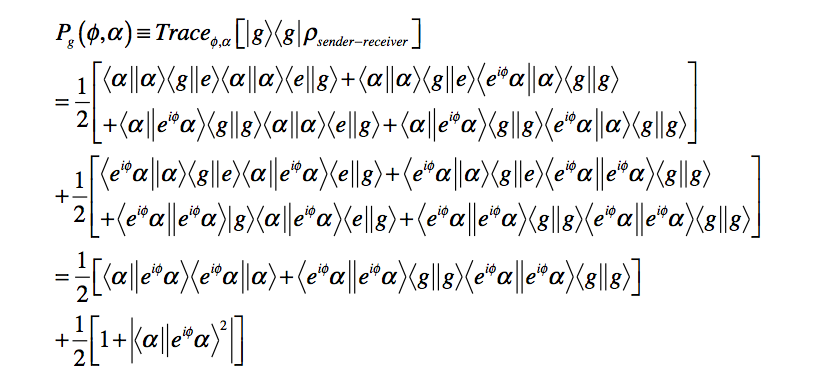
this is independent of the space-time interval separating detection of g from the choice of alpha and phi .


True, one cannot send FTL signals with entanglement using the ions in the Paul trap - unless somehow we can add a teleportation link. You have not considered that at all yet.
I accept that what you wrote here:
"(c) The selective dipole force of the coherent displacement beams excited the motion correlated with the |e> component to a state |alpha>". This is only possible if one has direct access to both components since one is selectively exciting only the motional state correlated with |e>."
is true in the ion-trap measurements, but it is still not a two point correlation in the sense of Aspect's measurements because data only from the internal qubit system teleported to Bob will allow Bob to see the message encoded by Sam-Alice without asking Sam-Alice for a secondary key. True this may not be FTL as yet, but even if inside the light cone the NST forbids it.
So again, my point is NOT that the ion-trap data shows FTL signals, but that it shows STL entanglement signals. All entanglement signals FTL, STL or retro-causal are verboten in the general NST.
The general NST says that given an entangled whole, no local measurement on one part of the whole, by itself, can depend on any controllable parameters on another part of the whole. That is, all such functional dependence must be erased locally and can only be decoded in hindsight with a secondary classical signal key that permits a correlation computation.
Begin forwarded message:
From: JACK SARFATTI <This email address is being protected from spambots. You need JavaScript enabled to view it.>
Subject: Re: dubious about sender control over phi
Date: March 17, 2012 6:49:47 PM PDT
To: REK
On Mar 17, 2012, at 4:17 PM, REKer wrote:
Again in the ion trap experiment it's not Alice that is manipulating phi or n but  what I'm calling 'Sam' (for 'source') in the form of phase-locked rf beams that manipulate the entire system:
That may be the case for that particular system, but that does not matter in the general case. What matters is that the local response depends on controllable parameters from the other end of the system. This itself is not possible in the no signal theorems. One can imagine that Sam and Alice are one and the same or very close together and that Bob is far away. Of course, that is not true for the trapped ion system, but that is not my point.
"The relative phases [phi and the phases of steps (b), (d), and (f)] of the steps above were controlled by phase locking the rf sources that created the frequency splitting of the Raman or displacement beams, respectively", just above eq (145)"
Fine, let that be Sam doing that and putting whatever message he wants in the time record for alpha and phi. That message is locally decodable by Bob only looking at his local measurements of the internal qubit. Bob does not have to communicate with Sam to unlock the message. The output from the internal quibts can be sent by any classical signal directly to Bob who can see the message without the key. At this point it does not matter that this communication is limited by light speed at all. That is a separate issue. The point of no signaling is not FTL, but that no kind of entanglement signaling even slower than light is possible. This is wrong - that's my point.
"The Raman beams clearly operate on the entire composite system according to their description.
And is also set by an operation on the composite system:
"(c) The selective dipole force of the coherent displacement beams excited the motion correlated with the |e> component to a state |alpha>". This is only possible if one has direct access to both components since one is selectively exciting only the motional state correlated with |e>. This means that the state |e> has to be distinguished from |g> in order to make that correlation. This is a local process, not something that Alice could do when spacelike separated from Bob.
It looks to me like steps (a) through (f) are all operations on the entire composite system.  I'm not saying that it's impossible for a sender Alice to modulate phi or n, but according to the article it is operations on the entire composite system space that are modulating phi and/or n.
What you are calling my 'intuitive' arguments are my attempts to make sure that your *physical* interpretation of the mathematics is consistent. Just because you see Alice's parameters changing does not mean that Alice can do this without causal access to Bob's system.  If you can really find a way for the sender only to modulate Phi or then you'd have something. But that's not what's being done in this experiment.
You are focusing too much on this example. What you don't seem to get is that any kind of entanglement signal is forbidden by the proofs. Getting outside the light cone is the next step - not the trapped ion system of course.
RK
On Mar 17, 2012, at 4:17 PM, REK  wrote:
Again in the ion trap experiment it's not Alice that is manipulating phi or n but  what I'm calling 'Sam' (for 'source') in the form of phase-locked rf beams that manipulate the entire system:
________________________________________
On Mar 17, 2012, at 10:59 AM, REK wrote:
What you have shown in your calculations is that the reduced density operator of the internal energy subspace is not necessarily proportional to the identity and that its form depends on phi.  But the fact that the reduced density matrix of the energy subspace can be different from the identity  doesn't necessarily mean that some sender Alice (the motion degree of freedom) can alter something in the receiver Bob's (energy levels) subspace.
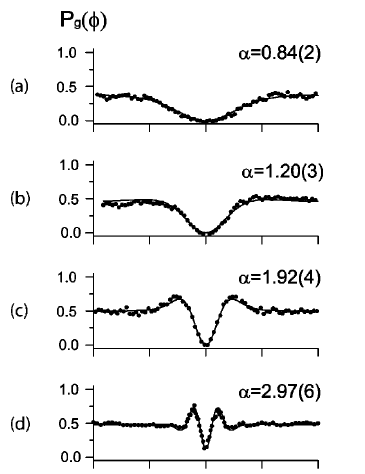
On the contrary I think it obviously does. Alice can manipulate phi as a function of time and that is a message that Bob sees locally without needing a classical signal key from Bob. I think Leibfried is explicit on how they control phi in order to get Fig 16 - will find that text later today. ;-)
Also you have forgotten that not only do they control Alice's relative phase phi but they also control Alice's signal intensity = |alpha|^2 they have four distinct intensities 0.84, 1.20, 1.92 & 2.97 as will as MANY phase phi DATA points - look closely at the graphs. This is obvious proof of precise control for both intensity and phase modulation of a message.