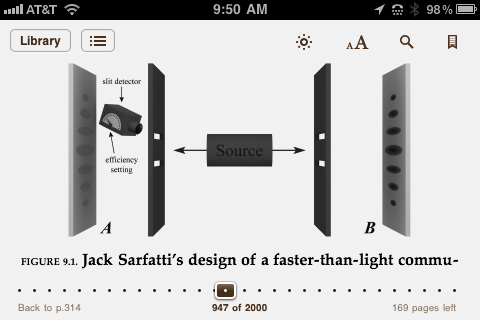
I am playing Devil's Advocate here just in case John Cramer's variation on the Dopfur experiment is correct and Henry's et-al's general no-signal proofs in OQT have a hidden flaw in them like John von Neumann's wrong proof against hidden variables.
My starting equation is
<x,x'|A,B> = <x|A1><x'|B2'> + e^i@(y)<x|A2><x'|B1'> (3)
the first term on the RHS is the sum of all Feynman histories where particle A of the entangled pair passes through slit 1 and lands on a point x on the screen AND particle B passes through slit 2' on the other side landing on the other screen at x'. The particles are emitted back to back. The random phase factor includes scatterers in the Heisenberg microscope and possible environmental decoherence. I suppress the unitary time translation operators or the Feynman propagators depending on which formalism one would use in detail. x includes the time of arrival. This is an important detail.
when the multiple integral with respect to y and x of
<A2|x,y><y,x|A1> = 0 (2)
this assumes that the integrals are taken at fixed times - that is a problem here because the alternative paths for a given single particle in an entangled pair will have different arrival times at the screen if they start with the same speed. Of course there will be an uncertainty in initial speeds as well. So the integrals for orthogonality only select the alternative histories for the same transit time from source to different points on the screen.
Of course in a real experiment one pair at a time, waiting for a build up of a pattern, this condition of same transit time is violated. So this is a conceptual problem. There is a similar problem for intense beams. And, of course, laser beam eigenstates are over-complete Glauber states and not mutually orthogonal for different Feynman histories.
I think you get effective nonunitarity if you integrate over the screen for different arrival times from the emission source!
In any case it seems obvious to me that the fringe pattern on the receiver side depends on the density matrix partial trace over the transmitter screen that is terms like
<A2|A1><B1'|x'><x'|B2'> (7)
Therefore, the key factor needed for no-signaling is the effective orthogonality condition
<A2|A1> = 0
